Mar 21, 2009
Originally posted on Half an Hour, March 21, 2009.
The Network Phenomenon: Empiricism and the New Connectionism
Stephen Downes, 1990
(The whole document in MS-Word)
TNP Part VII Previous Post
VIII. Associationism: Inferential Processes
A. The Structure in Review
Before proceeding to a description of associationist inferential structure, I would like to draw together some of the conclusions from preceding sections in order to outline the structure in which associationist inference occurs.
The computational structure follows a connectionist model. The system consists of interconnected units which are activated or inactivated according to external input and input via connections to each other. Such systems, I have noted, automatically, via various learning mechanisms, perform various associative tasks, for example, generalization. I have suggested that the human brain is actually constructed according to connectionist principles, therefore, the computational structure is actually built into the brain.
At the data level, mental representations are distributed representations, that is, no one unit contains a given representation, but rather, the representation consists of the set of connections between a given unit and a set of other units. This set of connections can be represented by a vector which displays the pattern of connectivity which activates the unit in question. Various representations cluster according to the similarity of their respective vectors, producing abstractions and categories.
External input to the system is entered via the senses. This input consists in the activation of what I have called real input units. This input is processed unconsciously according to connectionist principles and at a certain point we become conscious of this processing. At this point, I describe the set of activations as conscious input. We produce abstractions by processing conscious input. Any input from any sensory modality will consist of a pattern of unit activation. These patterns of activation are the input patterns for the vectors referred to above.
At no point in the system described thus far is anything like a symbol or a sentence expected or required. Categorization and abstraction from external input occurs as a form of subsymbolic processing. The data from which we form categories and abstractions consists not of symbols or sentences, but rather, the data consists of what may loosely be called pictures or mental images. Mental images, at leas at the conscious level, are formed by a conjunction of external input [and] input from previously formed associations at higher levels.
In all of this processing, no formal rules of inference are expected or required. Abstractions, generalizations and categorizations are formed automatically. One way of describing the process is to say that units with similar vectors will tend to be clustered. The same process can be described in a more complex manner with reference directly and only to the connectionist principles outlined above.
B. Inference by Prototype
Let me now describe the process of inference with reference to an example. Suppose we have constructed a prototype bird (which looks pretty much like a robin). This prototype consists of a unit which is connected to a set of other units, some of themselves may be prototypes. One of these prototypes, which happens to be strongly connected to the bird prototype., represents "flight".
Now for the inference part. Suppose we have a completely new experience, say, for example, an alien being walks off a spaceship. We see this, and this establishes a certain set of input patterns. The input patterns are such that a reasonable potion of the bird vector is activated (one might say, simplistically, that it looks like a bird). The activation of the bird unit in turn tends to activate all the units to which it is connected (that is, he activation of the bird unit consists in the activation of a partial vector for some other unit, which activates that unit, and which in the end results in the activation of the entire vector). Thus, in association with our perceiving an alien, the unit representing flight is activated. From our seeing an alien which looks like a bird, we have formed the expectation that it can fly.
There is reasonable evidence that something like this actually occurs. One clear example is the manner in which we stereotype people according to their skin colour or their country of origin. What is happening here is just an instance of inductive inference: from similar phenomena, we expect similar effects. This is not a rule-governed process. The occurrence and reliability of a particular inductive inference depends on the repetition of similar phenomena in previous experience (we have to have seen birds fly) and the particular set of mental representations in a given observer. Some of our previous experiences may inhibit our comparison of the alien with a bird, in which case, we might not form the expectation that it will fly.
For any given experience, various units at various levels of abstraction will be activated or inactivated. These units will be affected not only by the input experience but also by each other. Initial expectations may be revised according to activations at higher levels of abstraction (for example, we may initially expect the alien to be able to fly, but then only later remember that aliens never fly). The process being described here is similar to Pollock's system of prima facie knowledge and defeaters. [62] The difference is, first, we are not working with propositions as our items of knowledge, and second, anything can cunt as an instance of prima facie knowledge or a defeater, depending on patterns of connectivity and activation values. (But with Pollock, I would say that prima facie knowledge tends to be that produced by sensory input, and that defeaters tend to be produced by abstracted general knowledge.)
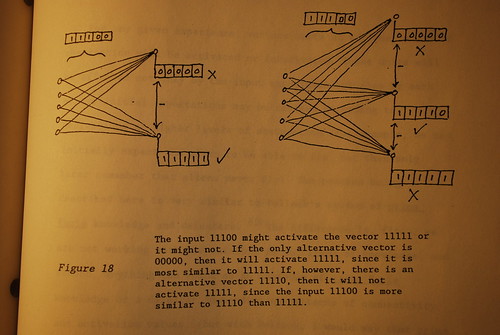
When we say that from similar phenomena we expect similar effects, it should be pointed out that this sort of inference need not apply only to similar cases where "similarity" is conceived to be similar appearance feel, sight, sound, etc.). We have a much more precise definition of similarity which can be employed here: two concept or representation units, each of which is associated with a particular vector, are similar if and only if their vectors overlap to a sufficient degree. Now I realize that "to a sufficient degree" is rather vague. In any given system, it can be predicted with mathematical certainty what input will activate what concept (that's what computer emulations do). However, there are no general principles which can describe 'sufficiency" since there are innumerable ways two units can have similar vectors. See figure 18.
C. Inferences About Abstract Entities
One of the major stumbling blocks for empirical and associationist theories is the problem of abstract entities. We talk about such unobserved abstracts as time, space, mass and even love, yet since there are no direct observations of such entities, there are no empirical bases for such inferences.
But now we are in a position to explain how humans reason about abstract or unobserved phenomena. Consider, for example, tim. A number of linguists have pointed out that humans appear to talk about these entities, and thence, to reason about them, in terms of metaphors. [63] So, for example, we think of time as linear distance, for example, a road. Or we think of time as a resource to be bought, sold, stolen and the like (think of the term "time theft", which is currently in vogue in business journals). We draw conclusions about the nature of time by analogy with the metaphor. So, for example, we might argue that since a journey has a beginning, an end, and a 'line' between them, so does time.
An interesting observation is that these inferences vary from culture to culture. For example, there is no analogue in "undeveloped" cultures to the metaphor of time as a resource. Hence, it is not surprising to see people from such cultures treating time quite differently. Some cultures have never developed the analogy of time as a journey, but rather, identify points in time according to events (even we do this to some degree, or example, "1990 AD"). If our knowledge about time and space were, as Kant suggests, determined a priori, then we should not expect differences in our understanding and reasonings about time. Yet these differences are verified observationally. Therefore, it seems reasonable to conclude that our knowledge about space and time is not a priori knowledge. It must be learned from experience.
One question which arises is the question fo why we would develop such concepts in the first place. In order to explain this, I must do a bit of borrowing from the arguments below, but let me sketch how this done for now. I will proceed by means of an example.
Consider "mass". Mass is unobserved, and indeed, unobservable. There are no direct measurements of mass to be had. Yet mass is central to most of our scientific theories and one of the central concepts not to be tossed aside by Einstein's revision of Newtonian physics. It appears, therefore, that Newton would have had to [have] intuitively or mystically 'discovered' mass. I think that we can allow that Newton observed such things as force and acceleration. Let me borrow from below, and say he could measure these. [64] By employing Mill's fourth method of induction, he would discover that force and acceleration are proportional. This suggests an equality, so he could borrow from previously established identities the idea that there might be a similar identity at work here. because he was seeking to establish an identity, he invented a new term, mass, which converts proportionality to an equation.
The idea is that Newton wanted his equations to 'look like' other successful equations such as those of Kepler and Galileo. In order to accomplish this, he needed to invent a new term. The question remains, of course, where did the invention come from? Computationally, if we compare the vector which represents the proportionality [of] force and acceleration and the vector which represents, say, some equation from Euclid, there will be a difference. This difference is itself a vector and is determinable by, say, XOR addition or whatever. A unit which is activated by this vector becomes, in the first instance, the vector which represents mass. Later, of course, when our understanding of mass becomes enhanced by other experiments, other scientists represent mass with quite different vectors.
This last remark is an important point. There is no one vector which represents abstracts such as time, mass, love and the like. Rather, each individual human may represent these abstracts in quite different ways, depending on the metaphors available. If these concepts were innate, then we would not expect people to have such differing concepts. Whether or not people do have different understandings of time, space and the like is empirically measurable. Therefore, again, there is a means of confirming empirically this theory as compared to innateness theories.
D. Grammar, Mathematics, and Formal Inference
The three systems of grammar, mathematics and formal inference have in common the fact that they are characterized according to a set of formal rules in which abstract terms stand for well formed formulae, terms, and the like. Here I am thinking of such diverse examples as Bever, Fodor and Garrett's "mirror image" language, modus ponens, transformation rules (which require an abstract "trace" to keep track of transformations), x+y = y+y, and the like. Since all of these systems employ abstract terms, they then pose a challenge for empirical and associationist theories.
It is possible to construct abstracts in a connectionist system, as I have shown above. These abstractions are useful when we want to describe formal systems. It is quite a different matter, however, to asset that we actually employ rules containing these abstract entities when we speak, reason or add. I suggest that we do not. Rather, each of, say, a "correct" logical inference or a "grammatical" sentence is a phenomenon which is sufficiently similar to some or another "exemplar" (as I call it) or prototype of such phenomena. Again, let me give an example in order to illustrate.
Suppose we want to teach people basic propositional logic. Either we show them a set of examples and say that inferences like these are good inferences, or we teach them the rules of inference and how to apply them. So if we want to teach, say, modus ponens, then either we give students a set fo examples such as "If I am in Edmonton then I am in Alberta, I am in Edmon, thus, I am in Alberta", or we give them the logical form "If A then B, A, thus B". According to what I suggest, we employ the former method, not the latter. The use of rules alone is insufficient to teach propositional logic; no logic text is or could be written without examples. Thus, the examples are used to teach propositional logic.
I argue that a person learns grammar in a similar fashion. A person is shown instances of correct sentences. Then, when she attempts to construct sentences of her own. she attempts to emulate what she has been shown. A particular sentence is constructed by the activation of several types of units, in particular, units which represent exemplar sentences, and units which represent concepts to be represented in the new sentence. Such behaviour looks like rule-based performance, bt that is because the new sentence will be similar to the old sentence.
This is a theory which can be tested empirically. In a population of students with similar skills, one group could be taught logic via rules and substitutions, while another could be taught by examples. If this theory is correct, then the group using examples should demonstrate better performance. Holland (et.al) describe a series of experiments in which rule-based learning is compared to example-based learning. [65] Their findings are that persons who are subjected to example-based learning do about as well as persons given only rules. The best results are obtained by a combination of the two methods. [66] In my opinion, their results are not conclusive. They use as subjects college students who (presumably) have been exposed to abstract reasoning. In such cases, the rules themselves can function as prototypes. This occurs in people who are used to working with symbolic notation, for example, students with a substantial computer science or mathematics background. Further experimentation would more neutral subjects would be useful.
Connectionist systems can be shown to learn by example. In one instance, a network was trained to predict the order of words in a sentence by having been given examples of correct sentences. [67] The idea here is that different types of words, for example, nouns, verbs, and so on, are used in different contexts. A given class of words, say, a noun, will be used in similar contexts. Words are clustered according to the similarity of the contexts in which they appear. Clustering is described above. When a similar context appears in the future, a pool of words is available for use. This pool consists of words which tend to be employed in similar contexts. Selection of the exact word may depend on broader constraints, for example, visual input.
Let me emphasize that while appropriate word selection may look like rule-based behaviour, it is not necessarily rule-based behaviour, and in connectionist machines it is certainly not rule-based behaviour. As Johnson-Laird writes, "what evidence is there for mental representation of explicit grammatical rules? The answer is: people produce and understand sentences that appear to follow such rules, and their judgments about sentences appear to be governed by them. But that is all. What is left open is the possibility that formal rules of grammar are not to be found inside the head, just as formal rules of logic are not to be found there." [68]
I would like to suggest at this point that the theory that people learn formal systems by exemplar provides a solution to the Bever-Fodor-Garrett problem described above. Recall that the problem was to explain how people can determine whether or not a given string of letters is a wff in a mirror-image language. The problem for the empirical or connectionist approach was that, in order to explain how this is done, it was necessary to postulate that people follow a set of rules containing abstract [entities]. Yet, since associationism (which, of course, is characteristic o empirical and connectionist systems) is constrained by the "terminal meta-postulate", which stipulates that no term not used in the description of the input can be used in the description of the rule.
It is possible merely to deny the postulate and construct a finite-state algorithm, as Anderson and Bower have done. [69] In such a case it would be necessary to construct abstracts from partial vectors as described above. However, it is much more natural and direct to use examples of mirror-image languages to teach a connectionist system. This would be an interesting test for connectionism (and if it worked, a conclusive refutation of the problem). But I do not believe it will be that simple.
Recall ow Bever, Fodor and garret introduced the language: it is a mirror-image language. When they introduce the language in this way, they call to the reader's mind past recollection of mirrors and how they work. While the language does not, in a technical sense, preserve mirror images (the letters are not reversed), there is in a sense an analogy between the performance of mirrors and wffs in the language. In order to adequately test a connectionist system, this information would have to be provided. Clearly, this would be a complex problem. Let me suggest, however, in the absence of an experiment, that there is no a priori reason why a connectionist system, given the relevant information, could not solve this problem.
In my opinion, this is a problem common to many of the challenges to associationism. It is perhaps true that in a narrowly defined context, no associationist system can solve this or that problem. But humans do not work in narrowly defined contexts. In order to adequately test a connectionist system, it is necessary to provide the context.
E. Operationalism
The way to think of such diverse behaviours as riding a bicycle, speaking a sentence, or solving mathematical equations is to think of such behaviours as learned behaviours, learned from examples and by practice and correction. There is a wealth of literature in diverse areas which makes this same point. Kripke's account of Wittgenstein on rules is explicit about the need for practice and correction. Polanyi represents knowledge as a skill, like riding a bicycle, which can be practiced but not described. Dreyfus and Dreyfus talk about expert knowledge as being, in a manner of speaking, intuitive. Kuhn writes that learning science is not a matter of learning formulae, it's a matter of learning how to solve the problems at the back of the book. educational and psychological literature standardly speaks of knowledge being "internalized".
What I am proposing here has its similarities to a movement in the philosophy of science called "Operationalism". First clearly formulated by Bridgeman [70] it was a modified considerably by Carnap. [71] It is difficult to disentangle early operationalism from some of the Logical Positivist theses with which it is associated, for example, reductionism. In its first formulation, the idea of operationalism is to reduce all physical concepts and terms to operations. What I propose is a modification: all formal concepts and terms shoudl be understood as operations. There are several contemporary versions of operationalism. For example, Kitcher, using Mill's axioms as a starting point, formalizes mathematical knowledge in terms of operations. [72] Similarly, Johnson-Laird describes what he calls a "procedural semantics".
The key objection to operationalism - and indeed, to much of what I am proposing in this paper - was stated by L.J. Russell in his review of Bridgeman. Russell noted that scientists often consider one type of operation to be better than another. Therefore, operations are evaluated according to something over and above themselves. A similar critiism coul be made o Kitcher' axioms. Consider set theory. According to Kitcher, we define a set according to the operations of grouping or collecting. However, the objection runs, some groupings are better than others. For example, we prefer a grouping which collects ducks, robins and crows to one which collects typewriter[s], rocks and sheep. Therefore, something over and above any given operation of collecting is employed in order to evaluate that operation.
This is a very general objection to connectionism and deserved a section of its own.
TNP Part IX Next Post
[62] Pollock
[63] George Lakoff, Women, Fire and Dangerous Things, surveys these results. See also Lakoff's "Connectionist Semantics" from the Connectionism conference, Simon Fraser University, 1990.
[64] That is, I still need to explain counting.
[65] Induction, pp. 273-279. They cite Cheng, Holyoak, Nisbett, and Oliver (1986), "pragmatic versus Syntactic Approaches to Training Deductive Reasoning". Cognitive Psychology 16.
[66] Induction, p.276.
[67] Jeff Elman, "Representation in Connectionist Models", Connectionism conference, Smon Fraser University, 1990.
[68] Philip Johnson-Laird, The Computer and the Mind, p. 326.
[69] John Anderson and Gordon Bower, Human Associative Memory, pp. 12-16.
[70] Logic of Modern Physics.
[71] "The Methodological Character of Theoretical Concepts".
[72] Philip Kitcher, The Nature of Mathematical Knowledge.
[73] The Computer and the Mind.
The Network Phenomenon: Empiricism and the New Connectionism
Stephen Downes, 1990
(The whole document in MS-Word)
TNP Part VII Previous Post
VIII. Associationism: Inferential Processes
A. The Structure in Review
Before proceeding to a description of associationist inferential structure, I would like to draw together some of the conclusions from preceding sections in order to outline the structure in which associationist inference occurs.
The computational structure follows a connectionist model. The system consists of interconnected units which are activated or inactivated according to external input and input via connections to each other. Such systems, I have noted, automatically, via various learning mechanisms, perform various associative tasks, for example, generalization. I have suggested that the human brain is actually constructed according to connectionist principles, therefore, the computational structure is actually built into the brain.
At the data level, mental representations are distributed representations, that is, no one unit contains a given representation, but rather, the representation consists of the set of connections between a given unit and a set of other units. This set of connections can be represented by a vector which displays the pattern of connectivity which activates the unit in question. Various representations cluster according to the similarity of their respective vectors, producing abstractions and categories.
External input to the system is entered via the senses. This input consists in the activation of what I have called real input units. This input is processed unconsciously according to connectionist principles and at a certain point we become conscious of this processing. At this point, I describe the set of activations as conscious input. We produce abstractions by processing conscious input. Any input from any sensory modality will consist of a pattern of unit activation. These patterns of activation are the input patterns for the vectors referred to above.
At no point in the system described thus far is anything like a symbol or a sentence expected or required. Categorization and abstraction from external input occurs as a form of subsymbolic processing. The data from which we form categories and abstractions consists not of symbols or sentences, but rather, the data consists of what may loosely be called pictures or mental images. Mental images, at leas at the conscious level, are formed by a conjunction of external input [and] input from previously formed associations at higher levels.
In all of this processing, no formal rules of inference are expected or required. Abstractions, generalizations and categorizations are formed automatically. One way of describing the process is to say that units with similar vectors will tend to be clustered. The same process can be described in a more complex manner with reference directly and only to the connectionist principles outlined above.
B. Inference by Prototype
Let me now describe the process of inference with reference to an example. Suppose we have constructed a prototype bird (which looks pretty much like a robin). This prototype consists of a unit which is connected to a set of other units, some of themselves may be prototypes. One of these prototypes, which happens to be strongly connected to the bird prototype., represents "flight".
Now for the inference part. Suppose we have a completely new experience, say, for example, an alien being walks off a spaceship. We see this, and this establishes a certain set of input patterns. The input patterns are such that a reasonable potion of the bird vector is activated (one might say, simplistically, that it looks like a bird). The activation of the bird unit in turn tends to activate all the units to which it is connected (that is, he activation of the bird unit consists in the activation of a partial vector for some other unit, which activates that unit, and which in the end results in the activation of the entire vector). Thus, in association with our perceiving an alien, the unit representing flight is activated. From our seeing an alien which looks like a bird, we have formed the expectation that it can fly.
There is reasonable evidence that something like this actually occurs. One clear example is the manner in which we stereotype people according to their skin colour or their country of origin. What is happening here is just an instance of inductive inference: from similar phenomena, we expect similar effects. This is not a rule-governed process. The occurrence and reliability of a particular inductive inference depends on the repetition of similar phenomena in previous experience (we have to have seen birds fly) and the particular set of mental representations in a given observer. Some of our previous experiences may inhibit our comparison of the alien with a bird, in which case, we might not form the expectation that it will fly.
For any given experience, various units at various levels of abstraction will be activated or inactivated. These units will be affected not only by the input experience but also by each other. Initial expectations may be revised according to activations at higher levels of abstraction (for example, we may initially expect the alien to be able to fly, but then only later remember that aliens never fly). The process being described here is similar to Pollock's system of prima facie knowledge and defeaters. [62] The difference is, first, we are not working with propositions as our items of knowledge, and second, anything can cunt as an instance of prima facie knowledge or a defeater, depending on patterns of connectivity and activation values. (But with Pollock, I would say that prima facie knowledge tends to be that produced by sensory input, and that defeaters tend to be produced by abstracted general knowledge.)
When we say that from similar phenomena we expect similar effects, it should be pointed out that this sort of inference need not apply only to similar cases where "similarity" is conceived to be similar appearance feel, sight, sound, etc.). We have a much more precise definition of similarity which can be employed here: two concept or representation units, each of which is associated with a particular vector, are similar if and only if their vectors overlap to a sufficient degree. Now I realize that "to a sufficient degree" is rather vague. In any given system, it can be predicted with mathematical certainty what input will activate what concept (that's what computer emulations do). However, there are no general principles which can describe 'sufficiency" since there are innumerable ways two units can have similar vectors. See figure 18.

Figure 18. Similarity depends on the range of relevant alternatives.
C. Inferences About Abstract Entities
One of the major stumbling blocks for empirical and associationist theories is the problem of abstract entities. We talk about such unobserved abstracts as time, space, mass and even love, yet since there are no direct observations of such entities, there are no empirical bases for such inferences.
But now we are in a position to explain how humans reason about abstract or unobserved phenomena. Consider, for example, tim. A number of linguists have pointed out that humans appear to talk about these entities, and thence, to reason about them, in terms of metaphors. [63] So, for example, we think of time as linear distance, for example, a road. Or we think of time as a resource to be bought, sold, stolen and the like (think of the term "time theft", which is currently in vogue in business journals). We draw conclusions about the nature of time by analogy with the metaphor. So, for example, we might argue that since a journey has a beginning, an end, and a 'line' between them, so does time.
An interesting observation is that these inferences vary from culture to culture. For example, there is no analogue in "undeveloped" cultures to the metaphor of time as a resource. Hence, it is not surprising to see people from such cultures treating time quite differently. Some cultures have never developed the analogy of time as a journey, but rather, identify points in time according to events (even we do this to some degree, or example, "1990 AD"). If our knowledge about time and space were, as Kant suggests, determined a priori, then we should not expect differences in our understanding and reasonings about time. Yet these differences are verified observationally. Therefore, it seems reasonable to conclude that our knowledge about space and time is not a priori knowledge. It must be learned from experience.
One question which arises is the question fo why we would develop such concepts in the first place. In order to explain this, I must do a bit of borrowing from the arguments below, but let me sketch how this done for now. I will proceed by means of an example.
Consider "mass". Mass is unobserved, and indeed, unobservable. There are no direct measurements of mass to be had. Yet mass is central to most of our scientific theories and one of the central concepts not to be tossed aside by Einstein's revision of Newtonian physics. It appears, therefore, that Newton would have had to [have] intuitively or mystically 'discovered' mass. I think that we can allow that Newton observed such things as force and acceleration. Let me borrow from below, and say he could measure these. [64] By employing Mill's fourth method of induction, he would discover that force and acceleration are proportional. This suggests an equality, so he could borrow from previously established identities the idea that there might be a similar identity at work here. because he was seeking to establish an identity, he invented a new term, mass, which converts proportionality to an equation.
The idea is that Newton wanted his equations to 'look like' other successful equations such as those of Kepler and Galileo. In order to accomplish this, he needed to invent a new term. The question remains, of course, where did the invention come from? Computationally, if we compare the vector which represents the proportionality [of] force and acceleration and the vector which represents, say, some equation from Euclid, there will be a difference. This difference is itself a vector and is determinable by, say, XOR addition or whatever. A unit which is activated by this vector becomes, in the first instance, the vector which represents mass. Later, of course, when our understanding of mass becomes enhanced by other experiments, other scientists represent mass with quite different vectors.
This last remark is an important point. There is no one vector which represents abstracts such as time, mass, love and the like. Rather, each individual human may represent these abstracts in quite different ways, depending on the metaphors available. If these concepts were innate, then we would not expect people to have such differing concepts. Whether or not people do have different understandings of time, space and the like is empirically measurable. Therefore, again, there is a means of confirming empirically this theory as compared to innateness theories.
D. Grammar, Mathematics, and Formal Inference
The three systems of grammar, mathematics and formal inference have in common the fact that they are characterized according to a set of formal rules in which abstract terms stand for well formed formulae, terms, and the like. Here I am thinking of such diverse examples as Bever, Fodor and Garrett's "mirror image" language, modus ponens, transformation rules (which require an abstract "trace" to keep track of transformations), x+y = y+y, and the like. Since all of these systems employ abstract terms, they then pose a challenge for empirical and associationist theories.
It is possible to construct abstracts in a connectionist system, as I have shown above. These abstractions are useful when we want to describe formal systems. It is quite a different matter, however, to asset that we actually employ rules containing these abstract entities when we speak, reason or add. I suggest that we do not. Rather, each of, say, a "correct" logical inference or a "grammatical" sentence is a phenomenon which is sufficiently similar to some or another "exemplar" (as I call it) or prototype of such phenomena. Again, let me give an example in order to illustrate.
Suppose we want to teach people basic propositional logic. Either we show them a set of examples and say that inferences like these are good inferences, or we teach them the rules of inference and how to apply them. So if we want to teach, say, modus ponens, then either we give students a set fo examples such as "If I am in Edmonton then I am in Alberta, I am in Edmon, thus, I am in Alberta", or we give them the logical form "If A then B, A, thus B". According to what I suggest, we employ the former method, not the latter. The use of rules alone is insufficient to teach propositional logic; no logic text is or could be written without examples. Thus, the examples are used to teach propositional logic.
I argue that a person learns grammar in a similar fashion. A person is shown instances of correct sentences. Then, when she attempts to construct sentences of her own. she attempts to emulate what she has been shown. A particular sentence is constructed by the activation of several types of units, in particular, units which represent exemplar sentences, and units which represent concepts to be represented in the new sentence. Such behaviour looks like rule-based performance, bt that is because the new sentence will be similar to the old sentence.
This is a theory which can be tested empirically. In a population of students with similar skills, one group could be taught logic via rules and substitutions, while another could be taught by examples. If this theory is correct, then the group using examples should demonstrate better performance. Holland (et.al) describe a series of experiments in which rule-based learning is compared to example-based learning. [65] Their findings are that persons who are subjected to example-based learning do about as well as persons given only rules. The best results are obtained by a combination of the two methods. [66] In my opinion, their results are not conclusive. They use as subjects college students who (presumably) have been exposed to abstract reasoning. In such cases, the rules themselves can function as prototypes. This occurs in people who are used to working with symbolic notation, for example, students with a substantial computer science or mathematics background. Further experimentation would more neutral subjects would be useful.
Connectionist systems can be shown to learn by example. In one instance, a network was trained to predict the order of words in a sentence by having been given examples of correct sentences. [67] The idea here is that different types of words, for example, nouns, verbs, and so on, are used in different contexts. A given class of words, say, a noun, will be used in similar contexts. Words are clustered according to the similarity of the contexts in which they appear. Clustering is described above. When a similar context appears in the future, a pool of words is available for use. This pool consists of words which tend to be employed in similar contexts. Selection of the exact word may depend on broader constraints, for example, visual input.
Let me emphasize that while appropriate word selection may look like rule-based behaviour, it is not necessarily rule-based behaviour, and in connectionist machines it is certainly not rule-based behaviour. As Johnson-Laird writes, "what evidence is there for mental representation of explicit grammatical rules? The answer is: people produce and understand sentences that appear to follow such rules, and their judgments about sentences appear to be governed by them. But that is all. What is left open is the possibility that formal rules of grammar are not to be found inside the head, just as formal rules of logic are not to be found there." [68]
I would like to suggest at this point that the theory that people learn formal systems by exemplar provides a solution to the Bever-Fodor-Garrett problem described above. Recall that the problem was to explain how people can determine whether or not a given string of letters is a wff in a mirror-image language. The problem for the empirical or connectionist approach was that, in order to explain how this is done, it was necessary to postulate that people follow a set of rules containing abstract [entities]. Yet, since associationism (which, of course, is characteristic o empirical and connectionist systems) is constrained by the "terminal meta-postulate", which stipulates that no term not used in the description of the input can be used in the description of the rule.
It is possible merely to deny the postulate and construct a finite-state algorithm, as Anderson and Bower have done. [69] In such a case it would be necessary to construct abstracts from partial vectors as described above. However, it is much more natural and direct to use examples of mirror-image languages to teach a connectionist system. This would be an interesting test for connectionism (and if it worked, a conclusive refutation of the problem). But I do not believe it will be that simple.
Recall ow Bever, Fodor and garret introduced the language: it is a mirror-image language. When they introduce the language in this way, they call to the reader's mind past recollection of mirrors and how they work. While the language does not, in a technical sense, preserve mirror images (the letters are not reversed), there is in a sense an analogy between the performance of mirrors and wffs in the language. In order to adequately test a connectionist system, this information would have to be provided. Clearly, this would be a complex problem. Let me suggest, however, in the absence of an experiment, that there is no a priori reason why a connectionist system, given the relevant information, could not solve this problem.
In my opinion, this is a problem common to many of the challenges to associationism. It is perhaps true that in a narrowly defined context, no associationist system can solve this or that problem. But humans do not work in narrowly defined contexts. In order to adequately test a connectionist system, it is necessary to provide the context.
E. Operationalism
The way to think of such diverse behaviours as riding a bicycle, speaking a sentence, or solving mathematical equations is to think of such behaviours as learned behaviours, learned from examples and by practice and correction. There is a wealth of literature in diverse areas which makes this same point. Kripke's account of Wittgenstein on rules is explicit about the need for practice and correction. Polanyi represents knowledge as a skill, like riding a bicycle, which can be practiced but not described. Dreyfus and Dreyfus talk about expert knowledge as being, in a manner of speaking, intuitive. Kuhn writes that learning science is not a matter of learning formulae, it's a matter of learning how to solve the problems at the back of the book. educational and psychological literature standardly speaks of knowledge being "internalized".
What I am proposing here has its similarities to a movement in the philosophy of science called "Operationalism". First clearly formulated by Bridgeman [70] it was a modified considerably by Carnap. [71] It is difficult to disentangle early operationalism from some of the Logical Positivist theses with which it is associated, for example, reductionism. In its first formulation, the idea of operationalism is to reduce all physical concepts and terms to operations. What I propose is a modification: all formal concepts and terms shoudl be understood as operations. There are several contemporary versions of operationalism. For example, Kitcher, using Mill's axioms as a starting point, formalizes mathematical knowledge in terms of operations. [72] Similarly, Johnson-Laird describes what he calls a "procedural semantics".
The key objection to operationalism - and indeed, to much of what I am proposing in this paper - was stated by L.J. Russell in his review of Bridgeman. Russell noted that scientists often consider one type of operation to be better than another. Therefore, operations are evaluated according to something over and above themselves. A similar critiism coul be made o Kitcher' axioms. Consider set theory. According to Kitcher, we define a set according to the operations of grouping or collecting. However, the objection runs, some groupings are better than others. For example, we prefer a grouping which collects ducks, robins and crows to one which collects typewriter[s], rocks and sheep. Therefore, something over and above any given operation of collecting is employed in order to evaluate that operation.
This is a very general objection to connectionism and deserved a section of its own.
TNP Part IX Next Post
[62] Pollock
[63] George Lakoff, Women, Fire and Dangerous Things, surveys these results. See also Lakoff's "Connectionist Semantics" from the Connectionism conference, Simon Fraser University, 1990.
[64] That is, I still need to explain counting.
[65] Induction, pp. 273-279. They cite Cheng, Holyoak, Nisbett, and Oliver (1986), "pragmatic versus Syntactic Approaches to Training Deductive Reasoning". Cognitive Psychology 16.
[66] Induction, p.276.
[67] Jeff Elman, "Representation in Connectionist Models", Connectionism conference, Smon Fraser University, 1990.
[68] Philip Johnson-Laird, The Computer and the Mind, p. 326.
[69] John Anderson and Gordon Bower, Human Associative Memory, pp. 12-16.
[70] Logic of Modern Physics.
[71] "The Methodological Character of Theoretical Concepts".
[72] Philip Kitcher, The Nature of Mathematical Knowledge.
[73] The Computer and the Mind.



