Apr 16, 2010
Originally posted on Half an Hour, April 16, 2010.
You are probably one of those who believes that people become rich or famous or powerful because they deserve to be rich or famous or powerful.
Though there may be some minimal conditions (you have to be at least literate, for example, and you may, like George W. Bush, need to be at least a 'C' student) this assertion is for the most part false.
In fact, aside from any unfair advantage an individual may gain (as a result of already being rich, or being related to someone who is already famous, say) the most crucial condition is luck. Being in the right place at the right time.
To illustrate this, let's look at your iPod or MP3 player. You have, say, 1000 songs on your player. If you choose 'shuffle' the player will choose which song to play. And the player also counts how often you've played each song.
If it's all completely random, then if you play 10000 songs, then each song should have played about 10 times. Chance and probability means they won't work out to exactly 10 plays each, but there won't be a lot of variability. Play a million songs, and each song will play a thousand times each, give or take a few dozen.
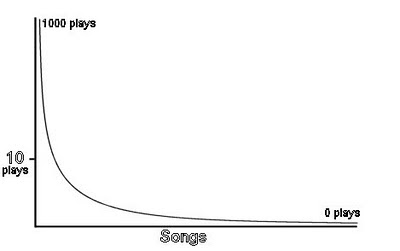
If we ordered the songs by how often they were played, and mapped out how frequently they were played, our chart would look like this:
Of course, it won't look exactly like that. You might choose to listen to your favorite songs a few times more. And, if you're like me, there are some songs you just want to skip past. So there will be a bit of a head and a bit of a tail to our graph.
Still, overall, things are pretty balanced. Which is what you would expect - and what you would want, of your random song selection.
Suppose, however, you want to tilt the playing field a bit. Instead of selecting completely randomly, suppose you include a slight preference to songs you've already played. To, say, a song would have a 10 percent greater chance of being selected if a song were played 10 times more than another.
Sounds great, right? The best songs will play more frequently, and the duds will never be played at all. Right?
Well, no - not unless you have already seeded all the 'song play' values first. Otherwise, if you let your new 'tilted' random song selector to operate on its own, a funny thing will happen.
The first few songs - whatever they are - will receive a slight benefit. This slight benefit will multiply, bit by bit, as the song selector picks them over other songs. It will grow and grow and grow until the selector is playing almost nothing but the first few songs. Any song not lucky enough to have been selected first will not be selected at all.
If we create the same graph we did before, we get what is known as a 'power law' graph, where the few that are played frequently create a big spike, and the remainder, that are played rarely, if at all, form a long tail.
Well, no problem, right? This is exactly what happens with popular songs, well-known websites, the distribution of wealth, and many more things in society. It's the most natural thing in the world.
Sure. But - crucially - what would happen if you tried the same experiment on your iPod a second time, you would get exactly the same spike, but with different songs. Do it again, and you get different songs again.
This system will always select a favorite and promote it to the top of the big spike, but this selection is purely random; it has nothing to do with the song itself. Even if you're selecting a song yourself to listen to from time to time, the preferential selection will still promote song after random song to the top of the heap.
What would you say, then, about the song at the top of the big spike? That it 'deserved' to be there? That it had the greatest 'merit' of any of the songs? No, of course not. You can't say anything about the song, except for the fact that, once it got a bit of an advantage, it was able to take off.
Even if you seed the selections with some favoured songs, the results will be all out of proportion over the preference. The longer the selective attractor runs, the greater these songs will be favoured. You might not want to listen to the same ten songs over and over - they're not that much better - but that's what will happen if the system is allowed to run long enough.
In fact, that's exactly what happens on popular radio. People tend to prefer to listen to a song that's familiar. This system, allowed to propagate long enough - over three decades, say - produces a global preference for a small set of 'classic' songs - and thus is born 'classic rock radio', which is almost all that can be found in some markets.
Are these songs so much better than all others that they should be played almost exclusively? No, of course not. Go to Indie or free music sites like Jamendo and you'll find some songs you like just as much as your classic rock favorites (at least, they will be, once you've listened to them a few times).
This is a phenomenon that can exist in networks generally. Yes, it is a natural phenomenon. As writers like Albert-László Barabási show, we see these in many places, from the formation of river systems to the distribution of limbs in a tree to the distribution of trails and roads.
But these effects do not exist because one option is better than the other. They exist because one option was lucky enough to be first, to be in the right place at the right time.
Whether it is the popularity of a politician, the influence of a song, the number of links received by a website, the viewership of a viral video, the wealth of a corporate tycoon, or any of a hundred other power law phenomena, the predominate characteristic of these is not greater quality or virtue or value, but a simple multiplier effect that could just as easily have chosen something else.
Don't equate wealth with knowledge, fame with insight. Don't equate the accidental properties of a network phenomenon to intrinsic worth or value. The differences between us are far slighter than the disparities in wealth, power or fame would indicate. We are all much more similar than we are dissimilar.
You are probably one of those who believes that people become rich or famous or powerful because they deserve to be rich or famous or powerful.
Though there may be some minimal conditions (you have to be at least literate, for example, and you may, like George W. Bush, need to be at least a 'C' student) this assertion is for the most part false.
In fact, aside from any unfair advantage an individual may gain (as a result of already being rich, or being related to someone who is already famous, say) the most crucial condition is luck. Being in the right place at the right time.
To illustrate this, let's look at your iPod or MP3 player. You have, say, 1000 songs on your player. If you choose 'shuffle' the player will choose which song to play. And the player also counts how often you've played each song.
If it's all completely random, then if you play 10000 songs, then each song should have played about 10 times. Chance and probability means they won't work out to exactly 10 plays each, but there won't be a lot of variability. Play a million songs, and each song will play a thousand times each, give or take a few dozen.
If we ordered the songs by how often they were played, and mapped out how frequently they were played, our chart would look like this:
Of course, it won't look exactly like that. You might choose to listen to your favorite songs a few times more. And, if you're like me, there are some songs you just want to skip past. So there will be a bit of a head and a bit of a tail to our graph.
Still, overall, things are pretty balanced. Which is what you would expect - and what you would want, of your random song selection.
Suppose, however, you want to tilt the playing field a bit. Instead of selecting completely randomly, suppose you include a slight preference to songs you've already played. To, say, a song would have a 10 percent greater chance of being selected if a song were played 10 times more than another.
Sounds great, right? The best songs will play more frequently, and the duds will never be played at all. Right?
Well, no - not unless you have already seeded all the 'song play' values first. Otherwise, if you let your new 'tilted' random song selector to operate on its own, a funny thing will happen.
The first few songs - whatever they are - will receive a slight benefit. This slight benefit will multiply, bit by bit, as the song selector picks them over other songs. It will grow and grow and grow until the selector is playing almost nothing but the first few songs. Any song not lucky enough to have been selected first will not be selected at all.
If we create the same graph we did before, we get what is known as a 'power law' graph, where the few that are played frequently create a big spike, and the remainder, that are played rarely, if at all, form a long tail.
Well, no problem, right? This is exactly what happens with popular songs, well-known websites, the distribution of wealth, and many more things in society. It's the most natural thing in the world.
Sure. But - crucially - what would happen if you tried the same experiment on your iPod a second time, you would get exactly the same spike, but with different songs. Do it again, and you get different songs again.
This system will always select a favorite and promote it to the top of the big spike, but this selection is purely random; it has nothing to do with the song itself. Even if you're selecting a song yourself to listen to from time to time, the preferential selection will still promote song after random song to the top of the heap.
What would you say, then, about the song at the top of the big spike? That it 'deserved' to be there? That it had the greatest 'merit' of any of the songs? No, of course not. You can't say anything about the song, except for the fact that, once it got a bit of an advantage, it was able to take off.
Even if you seed the selections with some favoured songs, the results will be all out of proportion over the preference. The longer the selective attractor runs, the greater these songs will be favoured. You might not want to listen to the same ten songs over and over - they're not that much better - but that's what will happen if the system is allowed to run long enough.
In fact, that's exactly what happens on popular radio. People tend to prefer to listen to a song that's familiar. This system, allowed to propagate long enough - over three decades, say - produces a global preference for a small set of 'classic' songs - and thus is born 'classic rock radio', which is almost all that can be found in some markets.
Are these songs so much better than all others that they should be played almost exclusively? No, of course not. Go to Indie or free music sites like Jamendo and you'll find some songs you like just as much as your classic rock favorites (at least, they will be, once you've listened to them a few times).
This is a phenomenon that can exist in networks generally. Yes, it is a natural phenomenon. As writers like Albert-László Barabási show, we see these in many places, from the formation of river systems to the distribution of limbs in a tree to the distribution of trails and roads.
But these effects do not exist because one option is better than the other. They exist because one option was lucky enough to be first, to be in the right place at the right time.
Whether it is the popularity of a politician, the influence of a song, the number of links received by a website, the viewership of a viral video, the wealth of a corporate tycoon, or any of a hundred other power law phenomena, the predominate characteristic of these is not greater quality or virtue or value, but a simple multiplier effect that could just as easily have chosen something else.
Don't equate wealth with knowledge, fame with insight. Don't equate the accidental properties of a network phenomenon to intrinsic worth or value. The differences between us are far slighter than the disparities in wealth, power or fame would indicate. We are all much more similar than we are dissimilar.